Two friends in my 2-d Universe
So, I have now generalized the 2-d Universe a little more, and here are two particles interacting with each other within the surface of a sphere.
Cool, isn't it? So, how does one calculate such a pair of paths? As I mentioned previously, it's all standard non-Euclidean geometry and vectors and the like. So, let's go through the basics (and maths-types, please remember I am an astrophysicist and don't get grumpy about the words I use - it works :)).
Starting point is that we are on a sphere, and so it makes sense to use spherical polar coordinates. Now, one painful thing is that different people define which angle is ϑ and which is φ, so I will be following the convention shown in the top figure on Wikipedia. Remember, however, we are working in the surface of the sphere, and so we have no radial (r) coordinate.
If we have two infinitesimal displacements in our coordinate (and assuming a unit sphere for convenience), then the separation between the displaced coordinates is given by;
And this defines the terms in the metric of the surface. We can write this as a matrix (I can feel the mathmos blood starting to boil) of the form;
To calculate the motion, we need some equations of motion :) and for those, we use Christoffel symbols, which tell us the equations of motion are given by

where we are using the Einstein summation convention, and the greek characters are just our coordinates that we are using. The v-terms are velocities in our coordinate directions. If we plug all the terms in, calculating the Christoffel symbols, the equations of motion become;
Excellent. We can immediately see that if we plonk a particle down at rest (so its velocity terms are zero), these equations are zero. If the velocity is not zero, the particle will move over the sphere, but these equations are not zero, so the components of the velocity are changing. What does this mean for the path of the particle? It's not hard to show that the particle moves with a velocity of constant magnitude and covers a great circle path over the sphere, but here I will just show this graphically. Here's the same experiment with the magnitude of the interacting force set to zero.
As we expect, two great circles. But what about the components of the velocities? Let's just take an example path;
Here, the blue is the ϑ velocity, and the green is the φ, while the red is the magnitude of the velocity, which is constant. The important thing to remember is that we are not sitting on a flat, Euclidean surface with a cartesian coordinate system, and so the normalization of the velocity is not simply obtained using Pythagoras, but by
So, that all works. Particles happily travel through the spherical surface on effectively free-fall paths, covering great circles. But now we need to add the interaction between the particles, and for that we need to calculate a few things. Firstly, there is the distance between particles in the surface of the sphere! That's relatively straight-forward. Then we need to work out the vector components of the force, that is somewhat harder. Once we have these, we then use the modified form of the geodesic equation, which includes the influences of forces, that is
where the a terms are components of the acceleration. But I'll leave that for next time.
Cool, isn't it? So, how does one calculate such a pair of paths? As I mentioned previously, it's all standard non-Euclidean geometry and vectors and the like. So, let's go through the basics (and maths-types, please remember I am an astrophysicist and don't get grumpy about the words I use - it works :)).
Starting point is that we are on a sphere, and so it makes sense to use spherical polar coordinates. Now, one painful thing is that different people define which angle is ϑ and which is φ, so I will be following the convention shown in the top figure on Wikipedia. Remember, however, we are working in the surface of the sphere, and so we have no radial (r) coordinate.
If we have two infinitesimal displacements in our coordinate (and assuming a unit sphere for convenience), then the separation between the displaced coordinates is given by;
And this defines the terms in the metric of the surface. We can write this as a matrix (I can feel the mathmos blood starting to boil) of the form;
To calculate the motion, we need some equations of motion :) and for those, we use Christoffel symbols, which tell us the equations of motion are given by

where we are using the Einstein summation convention, and the greek characters are just our coordinates that we are using. The v-terms are velocities in our coordinate directions. If we plug all the terms in, calculating the Christoffel symbols, the equations of motion become;
Excellent. We can immediately see that if we plonk a particle down at rest (so its velocity terms are zero), these equations are zero. If the velocity is not zero, the particle will move over the sphere, but these equations are not zero, so the components of the velocity are changing. What does this mean for the path of the particle? It's not hard to show that the particle moves with a velocity of constant magnitude and covers a great circle path over the sphere, but here I will just show this graphically. Here's the same experiment with the magnitude of the interacting force set to zero.
As we expect, two great circles. But what about the components of the velocities? Let's just take an example path;
Here, the blue is the ϑ velocity, and the green is the φ, while the red is the magnitude of the velocity, which is constant. The important thing to remember is that we are not sitting on a flat, Euclidean surface with a cartesian coordinate system, and so the normalization of the velocity is not simply obtained using Pythagoras, but by
So, that all works. Particles happily travel through the spherical surface on effectively free-fall paths, covering great circles. But now we need to add the interaction between the particles, and for that we need to calculate a few things. Firstly, there is the distance between particles in the surface of the sphere! That's relatively straight-forward. Then we need to work out the vector components of the force, that is somewhat harder. Once we have these, we then use the modified form of the geodesic equation, which includes the influences of forces, that is
where the a terms are components of the acceleration. But I'll leave that for next time.

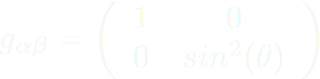





Comments
Post a Comment