Moving Charges and Magnetic Fields

Still struggling with grant writing season, so another post which has resulted in my random musings about the Universe (which actually happens quite a lot).

In second semester, I am teaching electricity and magnetism to our First Year Advanced Class. I really enjoy teaching this class as the kids are on the ball and can ask some deep and meaningful questions.

But the course is not ideal. Why? Because we teach from a textbook and the problem is that virtually all modern text books are almost the same. Science is trotted out in an almost historical progression. But it does not have to be taught that way.

In fact, it would be great if we could start with Hamiltonian and Lagrangian approaches, and derive physics from a top down approach. We're told that it's mathematically too challenging, but it really isn't. In fact, I would start with a book like The Theoretical Minimum, not some multicoloured compendium of physics.

We have to work with what we have!

One of the key concepts that we have to get across is that electricity and magnetism are not really two separate things, but are actually two sides of the same coin. And, in the world of classical physics, it was the outstanding work of James Clerk Maxwell who provided the mathematical framework that broad them together. Maxwell gave us his famous equations that underpin electro-magnetism.

Again, being the advanced class, we can go beyond this and look at the work that came after Maxwell, and that was the work by Albert Einstein, especially Special Theory of Relativity.

The wonderful thing about special relativity is that the mix of electric and magnetic fields depends upon the motion of an observer. One person sees a particular configuration of electric and magnetic fields, and another observer, moving relative to the first, will see a different mix of electric and magnetic fields.

This is nice to say, but what does it actually mean? Can we do anything with it to help understand electricity and magnetism a little more? I think so.

In this course (and EM courses in general) we spend a lot of time calculating the electric field of a static charge distribution. For this, we use the rather marvellous Gauss's law, that relates the electric field distribution to the underlying charges.

I've written about this wonderful law before, and should how you can use symmetries (i.e. nice simple shapes like spheres, boxes and cylinders) to calculate the electric field.

Then we come to the sources of magnetic field. And things, well, get messy. There are some rules we can use, but it's, well, as I said, messy.

We know that magnetic fields are due to moving charges, but what's the magnetic field of a lonely little charge moving on its own? Looks something like this

Where does this come from? And how do you calculate it? Is there an easier way?

And the answer is yes! The kids have done a touch of special relativity at high school and (without really knowing it in detail) have seen the Lorentz transformations. Now, introductory lessons on special relativity often harp on about swimming back and forth across rivers, or something like that, and have a merry dance before getting to the point. And the transforms are presented as a way to map coordinators from one observer to another, but they are much more powerful than that.

You can use them to transform vectors from one observers viewpoint to another. Including electric and magnetic fields. And these are simple algebra.

where we also have the famous Lorentz factor. So, what does this set of equations tell us? Well, if we have an observer who sees a particular electric field (Ex,Ey,Ez), and magnetic field (Bx,By,Bz), then an observer moving with a velocity v (in the x-direction) with see the electric and magnetic fields with the primed components.

Now, we know that the electric field of an isolated charge at rest is. We can use Gauss's law and it tells us that the field is spherically symmetrical and looks like this

The field drops off in strength with the square of the distance. What would be the electric and magnetic fields if this charge was trundling past us at a velocity v? Easy, we just use the Lorentz transforms to tell us. We know exactly what the electric field looks like of the charge at rest, and we know that, at rest, there is no magnetic field.

Being as lazy as I am, I didn't want to calculate anything by hand, so I chucked it into MATLAB, a mathematical environment that many students have access too. I'm not going to be an apologist for MATLAB's default graphics style (which I think sucks - but there are, with a bit of work, solutions).

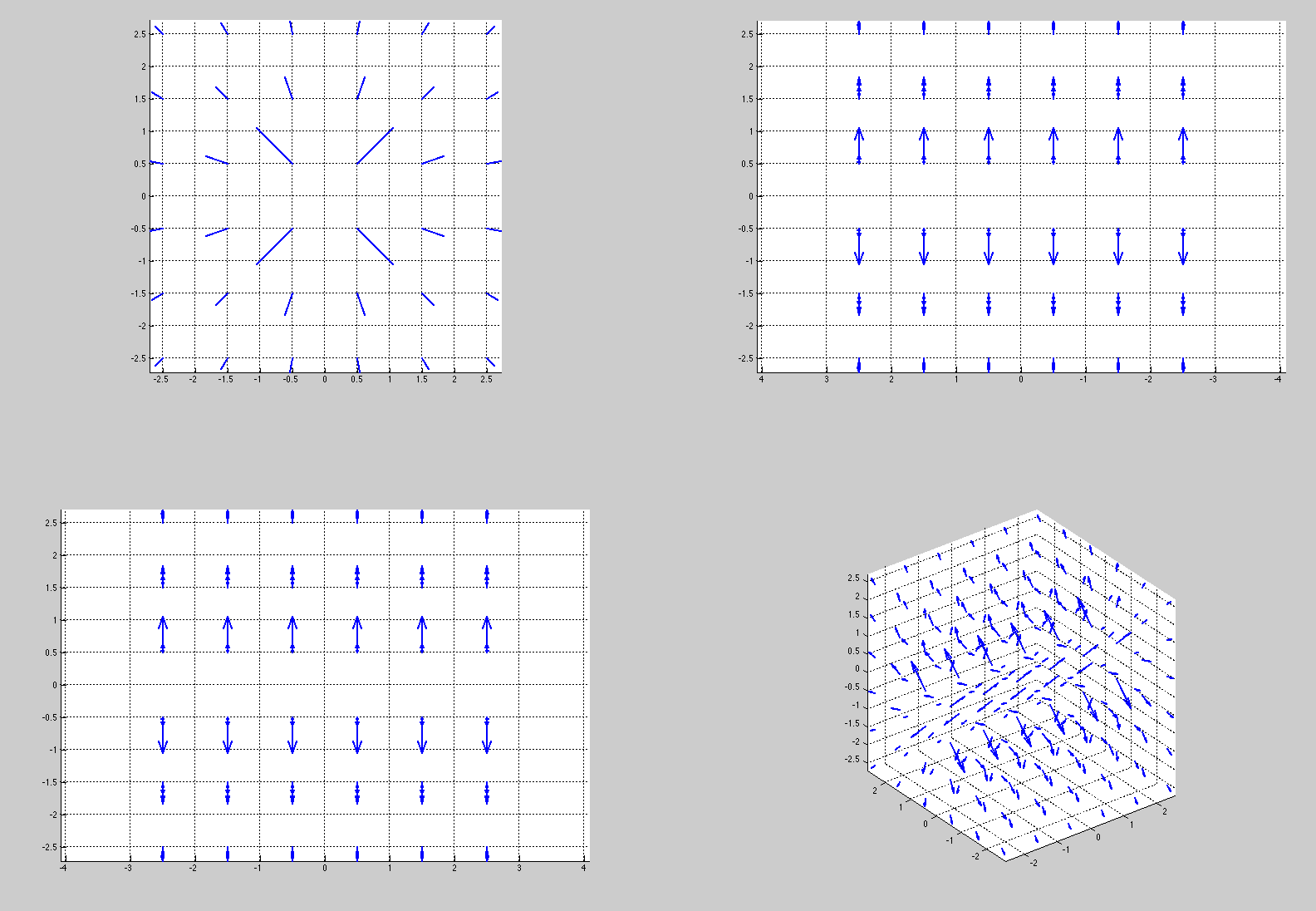
Anyway, here's a charge at rest. The blue arrows are the electric field. No magnetic field, remember!

So, top left is a view along the x-axis, then y, then z, then a 3-D view. Cool!

Now, what does this charge look like if it is moving relative to me? Throw it into the Lorentz transforms, and voila!

MAGNETIC FIELDS!!! The charge is moving along the x-axis with respect to me, and when we look along x we can see that the magnetic fields wrap around the direction of motion (remember your right hand grip rule kids!).

That was for a velocity of 10% the speed of light. Let's what it up to 99.999%

The electric field gets distorted also!

Students also use Gauss's law to calculate the electric field of an infinitely long line of charge. Now the strength of the field drops off as the inverse of the distance from the line of charge.

Now, let's consider an observer moving at a velocity relative to the line of charge.

Excellent! Similar to what we saw before, and what we would expect. The magnetic field curls around the moving line of charge (which, of course, is simply an electric current).

Didn't we know that, you say? Yes, but I think this is more powerful, not only to reveal the relativistic relationship between the electric and magnetic fields, but also once you have written the few lines of algebraic code in MATLAB (or python or whatever the kids are using these days) you can ask about more complicated situations. You can play with physics (which, IMHO, is how you really understand it).

So, to round off, what's the magnetic field of a perpendicular infinite line of charge moving with respect to you. I am sure you could, with a bit of work, calculate it with usual mathematical approaches, but let's just take a look.

Here's at rest

A bit like further up, but now pointing along a different axis.

Before we add velocity, you physicists and budding physicists make a prediction! Here goes! A tenth the velocity of light and we get

I dunno if we were expecting that! Remember, top left is looking along the x-axis, along the direction of motion. So we have created some magnetic structure. Just not the simple structure we normally see!

And now at 99.99% we get

And, of course, I could play with lots of other geometries, like what happens if you move a ring of charge etc. But let's not get too excited, and come back to that another day.