Battle of the Bayes
A little Saturday morning mathematical interlude.
There has been a few posts on the interwebs about an article by Brad Efron, a professor of statistics at Stanford University. The article appeared in the prestigious journal Science and has the title "Bayes Theorem in the 21st Century".
Ted Bunn has a good discussion of the paper over on his blog, and I suggest you have a read before you read what's below. But the paper continues to smoulder what is known as the Bayesian-Frequentist debate. It's a long winded debate (that some think doesn't even exist), but it all is focused on the question of "How do by prior beliefs change in the light of new data?". As ever, xkcd explains it perfectly;
(To explain, the frequentist worked out the change of a false positive based on the role of the dice, concluding that a YES was unlikely. The Bayesian, however, also considers the prior information of the chance that the Sun had gone nova during the experiment - as the chance of this is extremely small, the Bayesian can be confident of the bet).
Efron, however, brings up the usual complaint against Bayesian analysis, namely that the prior information is subjective - how much I think something is true might be different to you (as we have different information) - and people should be wary of Bayesian results.
Ted Bunn notes, before his analysis, that he has never taken a statistics course, and so it not really qualified to comment on the thoughts of a professor of statistics from Stanford. I, however, am substantially more qualified (I have an A/O-level in statistics which I got in High School, aged 17 - I think I got a B), so, while I am not a professor of statistics, I'll give it a go.
Identical or non-Identical Twins!
The example given by Efron is a nice, simple question. Imagine you're pregnant and you go for a scan. The doctor tells you that you will be having two baby boys, and the question hits you "Will they be identical twins, or fraternal?" (I guess you need to know this because if they are identical, you can save money by buying identical sets of clothes and freaking people out)!
Efron has been using this particular example for a while and is based on a true story.
How do we work this out? Well, you need some information. The first first thing is the proportion of twins that are identical. As Efron points out, this is a third, so we can write
No - there is a subtlety that we can't ignore, namely that identical twins can only be born in boy-boy or girl-girl combinations, whereas fraternal twins also have boy-girl combinations. So we can write this as
for the identical case, and
and we just plug everything in and find
So, the probability that the twin boys are identical is a half.
Everyone is happy with this, but Efron goes onto say that the problem is that we have used "prior" information" to make this calculation, namely the proportion of twin births that are identical. If we did not know this, we would assign an "uninformative prior" of there being a 50-50 chance of identical verses fraternal, and so we would get the above probability to be two-thirds, not a half, and hence wrong.
Because of this, Efron claims
I read this a few times, and think it's quite, errrm (being polite) misplaced (and the work frequentistically is freaky).
Let's think about it
Until I read the Efron article, I had no idea what the rates of identical verses fraternal twins was. There was a time when no one on Earth knew what the rates were. At some point, people started to record the details of births, and we could work these out.
So, let's go back in time and pretend all we know is that we have twin boys, but have no clue to the relative numbers of identical and fraternal twins. We can assume that the relative fraction is between between zero (where there is no identical twins) and 1 (where all twins are identical) and, but we have no preference of any particular value, so we have what's called a uniform prior.
The rest of what follows is very similar to how one would test whether a coin is fair. Let's see of we can see how this works with the picture below.
But we have two bits of information, so we multiply the probability distributions together and get the red curve. The chance for I=0 and I=1 are zero, and the probability peaks at I=0.5; it looks like there is a 50-50 chance for any particular birth to be identical.
Suddenly the crone says that she actually remembers many thousands of previous twin births, and starts to rattle off whether they were identical or not. As she does, you quickly add the data into our probability distributions and you notice that the distribution is becoming narrower and shifts away from having a centre at 0.5. After 10,000 remembered births, your distribution become the blue spikey curve, highly peaked at I=1/3. What you've deduced is that probability that twins being identical is a about a third.
But we still need to answer the question "What the probability that your twins are identical, in light of the knowledge that they are two boys?"
So, we can take the Bayesian formula up there and write it in terms of the number of births we have recorded that are identical (we'll call that number r) and fraternal (call that n). I won't go though the maths here, but the probability that your hypothesis that the twins are identical is true is;
So, when we knew nothing, so n=r=0, this is two-thirds. This is the uninformative prior result noted by Efron. What happens when we include the information from the crone? You get the following
The red dots are the recorded identical twins, and the blue dots are the recorded fraternal twins (x-axis should be number of reported twins plus one), and the green is the probability that your twins are identical. The first point starts off as two-thirds and bounces arounds as we collect more and more data, and approaches a half, as we expected from the above.
Wrapping it up
Hmm, this post has gotten to be much longer than I planned, so I think it's time to wrap this up.
I think what I want to reiterate is that I think Efron's comment is misplaced. Up there, I considered that I didn't know the chance of getting identical twins, but in reality, I could have easily expanded this to not knowing the chances of getting two boys as opposed to two girls, or even the relative shares in fraternal twins. The Bayesian framework is the way to continually update your beliefs in light new data.
OK - all of that may have seemed a little esoteric, but humans are Bayesians. For the local, here's an example based upon the race that stops a nation (I should point out, it doesn't stop me - I only like the Grand National).
Many people have a flutter, but don't know anything about the individual horses, and so are happy to be assigned a horse at random, or just pick one based upon something quirky, like the horse's name. If you are a little more racing-savvy (which I am not, I am not a gambling man), you might check out the odds - here, someone has looked at the history of the horses, and have assigned probabilities on how they think the race will be run; you will probably update your internal probabilities for betting on the horses.
However, if you are in the know, you might be privy to different information, such as the health of individual horses. Again, you will probably update your internal odds. As we have seen in Australia, often hiding prior information is considered naughty.
But the point is that there is no single "answer" to the probability distribution for the outcome of the race. Each person has a different distribution based upon their prior information. And, of course, this is not only in horse racing, but a huge range of human activities; the whole hoo-ha about insider dealing is that some people have information that make the playing field uneven.
In science, we start off with little bits of data and differing opinions on what they mean, but we continually collect data and update our probability distributions; this is why we continue to ask questions like is it really a Higgs Boson? The key point is that the data will overcome your prior distributions, and people agree on what we are seeing (although some people's prior distribution are so strong, no matter how much data we collect, they will cling to their ideas).
OK - it's now Sunday morning, and I am going to have some toast and promite. I am going to shamelessly finish this blog with a wonderful picture from Ted Bunn; controversial, but I can't help agree.
Thanks to the Gravitational Astrophysics Group and Brendon Brewer for invaluable input on this one.
There has been a few posts on the interwebs about an article by Brad Efron, a professor of statistics at Stanford University. The article appeared in the prestigious journal Science and has the title "Bayes Theorem in the 21st Century".
Ted Bunn has a good discussion of the paper over on his blog, and I suggest you have a read before you read what's below. But the paper continues to smoulder what is known as the Bayesian-Frequentist debate. It's a long winded debate (that some think doesn't even exist), but it all is focused on the question of "How do by prior beliefs change in the light of new data?". As ever, xkcd explains it perfectly;
(To explain, the frequentist worked out the change of a false positive based on the role of the dice, concluding that a YES was unlikely. The Bayesian, however, also considers the prior information of the chance that the Sun had gone nova during the experiment - as the chance of this is extremely small, the Bayesian can be confident of the bet).
Efron, however, brings up the usual complaint against Bayesian analysis, namely that the prior information is subjective - how much I think something is true might be different to you (as we have different information) - and people should be wary of Bayesian results.
Ted Bunn notes, before his analysis, that he has never taken a statistics course, and so it not really qualified to comment on the thoughts of a professor of statistics from Stanford. I, however, am substantially more qualified (I have an A/O-level in statistics which I got in High School, aged 17 - I think I got a B), so, while I am not a professor of statistics, I'll give it a go.
Identical or non-Identical Twins!
The example given by Efron is a nice, simple question. Imagine you're pregnant and you go for a scan. The doctor tells you that you will be having two baby boys, and the question hits you "Will they be identical twins, or fraternal?" (I guess you need to know this because if they are identical, you can save money by buying identical sets of clothes and freaking people out)!
Efron has been using this particular example for a while and is based on a true story.
How do we work this out? Well, you need some information. The first first thing is the proportion of twins that are identical. As Efron points out, this is a third, so we can write
where the I means identical, and the I with the bar over it means "not identical".
So there's your answer, isn't it? The chance that your two boys are identical is one third?
No - there is a subtlety that we can't ignore, namely that identical twins can only be born in boy-boy or girl-girl combinations, whereas fraternal twins also have boy-girl combinations. So we can write this as
for the identical case, and
for the fraternal case. The notation in there in the brackets, such as p(A|B), means "the probability of A given that B is true".
So, how do we work out the probability that your twins are identical? We use Bayes rule which says
So, the probability that the twin boys are identical is a half.
Everyone is happy with this, but Efron goes onto say that the problem is that we have used "prior" information" to make this calculation, namely the proportion of twin births that are identical. If we did not know this, we would assign an "uninformative prior" of there being a 50-50 chance of identical verses fraternal, and so we would get the above probability to be two-thirds, not a half, and hence wrong.
Because of this, Efron claims
I read this a few times, and think it's quite, errrm (being polite) misplaced (and the work frequentistically is freaky).
Let's think about it
Until I read the Efron article, I had no idea what the rates of identical verses fraternal twins was. There was a time when no one on Earth knew what the rates were. At some point, people started to record the details of births, and we could work these out.
So, let's go back in time and pretend all we know is that we have twin boys, but have no clue to the relative numbers of identical and fraternal twins. We can assume that the relative fraction is between between zero (where there is no identical twins) and 1 (where all twins are identical) and, but we have no preference of any particular value, so we have what's called a uniform prior.
To quote Miranda's friend Tilly, "bear with". The x-axis is the chance of identical twins, and the y-axis is the probability of that chance. The blue horizontal line is my "prior probability", which means that I think that any incidence of twins is likely. And as I know nothing else, that's it.
But then an old crone from the local village says to me that a woman just had twins and they were fraternal. Data, the sauce of science! What does it tell us? Well, clearly the chance of all twin births being identical must be zero.
So, let's consider the range of incidence of identical twins in the picture. If I=0, then the chance of getting the data we observed is 100%. If I=0.5 the chance of getting the data is 50%, and as we said, if I=1 then the chance of seeing the data is zero; basically, that bit of data has turned our blue line into the green line.
The crone (sorry, not sure why it ended up being a crone) then adds "oh, and there was another birth of twins, and they were identical". The argument is now the same, but the argument is reversed e.g. if I=0, the chance of getting the data would be zero, and if I=1, then it would be 100%.
Suddenly the crone says that she actually remembers many thousands of previous twin births, and starts to rattle off whether they were identical or not. As she does, you quickly add the data into our probability distributions and you notice that the distribution is becoming narrower and shifts away from having a centre at 0.5. After 10,000 remembered births, your distribution become the blue spikey curve, highly peaked at I=1/3. What you've deduced is that probability that twins being identical is a about a third.
But we still need to answer the question "What the probability that your twins are identical, in light of the knowledge that they are two boys?"
So, we can take the Bayesian formula up there and write it in terms of the number of births we have recorded that are identical (we'll call that number r) and fraternal (call that n). I won't go though the maths here, but the probability that your hypothesis that the twins are identical is true is;
So, when we knew nothing, so n=r=0, this is two-thirds. This is the uninformative prior result noted by Efron. What happens when we include the information from the crone? You get the following
The red dots are the recorded identical twins, and the blue dots are the recorded fraternal twins (x-axis should be number of reported twins plus one), and the green is the probability that your twins are identical. The first point starts off as two-thirds and bounces arounds as we collect more and more data, and approaches a half, as we expected from the above.
Wrapping it up
Hmm, this post has gotten to be much longer than I planned, so I think it's time to wrap this up.
I think what I want to reiterate is that I think Efron's comment is misplaced. Up there, I considered that I didn't know the chance of getting identical twins, but in reality, I could have easily expanded this to not knowing the chances of getting two boys as opposed to two girls, or even the relative shares in fraternal twins. The Bayesian framework is the way to continually update your beliefs in light new data.
OK - all of that may have seemed a little esoteric, but humans are Bayesians. For the local, here's an example based upon the race that stops a nation (I should point out, it doesn't stop me - I only like the Grand National).
Many people have a flutter, but don't know anything about the individual horses, and so are happy to be assigned a horse at random, or just pick one based upon something quirky, like the horse's name. If you are a little more racing-savvy (which I am not, I am not a gambling man), you might check out the odds - here, someone has looked at the history of the horses, and have assigned probabilities on how they think the race will be run; you will probably update your internal probabilities for betting on the horses.
However, if you are in the know, you might be privy to different information, such as the health of individual horses. Again, you will probably update your internal odds. As we have seen in Australia, often hiding prior information is considered naughty.
But the point is that there is no single "answer" to the probability distribution for the outcome of the race. Each person has a different distribution based upon their prior information. And, of course, this is not only in horse racing, but a huge range of human activities; the whole hoo-ha about insider dealing is that some people have information that make the playing field uneven.
In science, we start off with little bits of data and differing opinions on what they mean, but we continually collect data and update our probability distributions; this is why we continue to ask questions like is it really a Higgs Boson? The key point is that the data will overcome your prior distributions, and people agree on what we are seeing (although some people's prior distribution are so strong, no matter how much data we collect, they will cling to their ideas).
OK - it's now Sunday morning, and I am going to have some toast and promite. I am going to shamelessly finish this blog with a wonderful picture from Ted Bunn; controversial, but I can't help agree.
Thanks to the Gravitational Astrophysics Group and Brendon Brewer for invaluable input on this one.



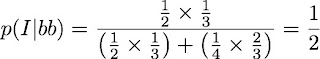



"But the point is that there is no single "answer" to the probability distribution for the outcome of the race. Each person has a different distribution based upon their prior information."
ReplyDeleteYep. I don't like it when people present this as a weakness of Bayesian Inference. IMO it's true whether you acknowledge it or not. Bayesian Inference forces you to acknowledge it. Supposed "alternative" methods can give the impression of not requiring prior information, which is absurd.
"I guess you need to know this because if they are identical, you can save money by buying identical sets of clothes and freaking people out"
ReplyDeleteI could follow all the statistics stuff, but this one got me stumped! I'm not aware of any children's clothes for which there is a discount if two identical items are bought. This would save money only in the following scenario: one claims to have only one child, and only one child at a time is seen, clothed, by the rest of the world, while the other child remains nude at home (or vice versa, of course). (This would also save money for fraternal twins, but one would have to keep the same one at home.)
I was assuming that you could get a discount if you buy identical wardrobes for identical twins (it seems they have often coordinated their entire clothing requirements). Even if you get fraternal twins to dress identically, they just ain't as freaky even when dressed the same way.
Delete