Falling into a Black Hole

For someone who works in relativity, you'd think I'd know where the time goes! Things have been quite busy with grants, Easter and packing up my office as the building I am in is to be demolished. We're going to be off campus for a couple of years, in the lovely suburb of Redfern; at least we'll be closer to the  train station :)

This has meant I've not had a lot of time to get a lot of research done, so I thought I would post a little lesson on relativity, namely what happens when you fall into a black hole. Not the painful bit where you get torn limb from limb, but what you see.

I've worked on this in the past, but this post was sparked by this article, especially this statement.

"First of all, you approach the speed of light as you fall into the black hole. So the faster you 

move through space, the slower you move through time," he said. "Furthermore, as you fall, there are things that have been falling in front of you that have experienced an even greater 'time dilation' than you have. So if you're able to look forward toward the black hole, you see every object that has fallen into it in the past. And then if you look backwards, you'll be able to see everything that will ever fall into the black hole behind you. 

"So the upshot is, you'll get to see the entire history of that spot in the universe simultaneously," he said, "from the Big Bang all the way into the distant future."

This is, to put it politely, simply wrong, and is a common misconception in relativity.

Firstly, a little history (and remember that I am not a historian of science). A black hole is a completely collapsed object, where gravity has overcome all other forces and the all the mass is compressed into a single point (the singularity - que stupid mystical wooooooo music).

The first person to write down the metric that describes the space-time of a black hole was Karl Schwarzschild in 1916. He realised that something weird occurred at the origin (the singularity - music again), but also at the "Schwarzschild Radius"

(pinched from wikipedia). The metric "blows up" at this point, and there appears to be another singularity. Unlike the singularity at the origin, the curvature of space-time at the Schwarzschild radius is well behaved. But it looked like this singularity stopped objects, both massive and photons, entering the black hole.

Hopefully this explains it

This shows radius along the x-axis, and time on the y-axis, and the solid lines are the paths of light rays. The central singularity is at r=0, and r=2m is the Schwarzschild radius. Notice that light rays are not moving at 45 degrees in this picture (which is what you get when you consider the flat space-time of special relativity). The key point is that light rays outside of r=2m stay outside, while those inside stay inside.

This confuddled many people, including Einstein, who concluded that black holes cannot form, as nothing can get inside them.

The problem was solved when it was realised that the problem at r=2m is a coordinate singularity, which is something like asking the question "What is north of the north pole?". With a change of coordinates, to Eddington-Finkelstein Coordinates, the situation at r=2m gets smoother out.

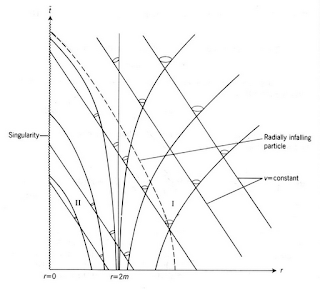
Now, what do you get for light rays?

There are some issues with this representation, as the "time" on the y-axis is more complicated than before. But the key point is that light rays from the outside can now cross to the inside. The light rays inside r=2m are stuck in there, showing that the Schwarzschild radius is an event horizon, a one-way membrane through which things can flow.

The dotted path shows what happens to an infalling observer. There are a couple of things you can see immediately from this picture;

• To see the entire future of the universe, the infalling observer would need to receive all of the inward traveling photons. Clearly, they hit r=0 (and certain death) before the top two photons reach them. So they only see a finite time into the future, not the entire future history of the universe.
• They can receive light from things that have fallen into the black hole before us, but we can't see thing outside from times before we fell in (well, no more than just seeing things far away in the past due to light travel times.

If you really want to understand, take a look at Andrew Hamilton's excellent webpage.

And if you're really looking to understand, you can have a read of my not-so-excellent paper

No Way Back: Maximizing survival time below the Schwarzschild event horizon

Geraint F. Lewis, Juliana Kwan

(Submitted on 8 May 2007 (v1), last revised 15 May 2007 (this version, v2))

It has long been known that once you cross the event horizon of a black hole, your destiny lies at the central singularity, irrespective of what you do. Furthermore, your demise will occur in a finite amount of proper time. In this paper, the use of rockets in extending the amount of time before the collision with the central singularity is examined. In general, the use of such rockets can increase your remaining time, but only up to a maximum value; this is at odds with the ``more you struggle, the less time you have'' statement that is sometimes discussed in relation to black holes. The derived equations are simple to solve numerically and the framework can be employed as a teaching tool for general relativity.