My Gyroscope won't fall down - I

I love this video

and used to do this very demo when teaching classical mechanics. But here's a question for you - why doesn't the wheel fall over?

If you trawl the text books, even the wonderful Feynman Lectures on Physics (a must read for any serious student of physics), the answer given is that the wheel doesn't fall down because of the conservation of angular momentum.

Alas, I think this answer is a bit of a cop out, and doesn't answer the question. Why? Let's consider the collision between two cars. We know from Newtonian mechanics that momentum is conserved, so the momentum before the collision is exactly the same as after the collision (let's ignore external forces for now, imagine the collision is on a frictionless sheet of ice).

The conservation of momentum is a consequence of Newton's third law, and in the collision all of the forces acting have equal and opposite reaction forces, with the total momentum unchanged. Basically, considering the conservation of momentum lets you ignore all of the forces going on in the collision.

But if you are one of the car drivers, you care implicitly about the forces acting, as you would very much prefer a gentle force acting on you over a long period (as provided by an air bag) as opposed to a larger force over a short period (as provided when your head hits the dashboard). 

The situation with the wheel is similar, as the action of the internal forces (well, torques) act so that the total angular moment is conserved. But really, to understand what's going on here, the question you should be asking is "what force is holding the wheel up?".

I know the answer, but would like to demonstrate it with a simplified model. Alas, the simplified model is not that simple, and it's going to take a few posts to get through, but basically I'm going to make a computer model of a wheel, spin it, let it go and look at where the forces are.

But firstly, a truth about the universe, namely that it is made from particles and springs

(taken from the excellent webpage of Paul Bourke, a place with excellent graphics advice). Now, this might sound weird, but you can represent physical material, and how they move etc, as a system of masses connected by springs. Check this out

and read the tutorial here. I wish I had realised this when I did my course on vibrations and waves as an undergraduate :)

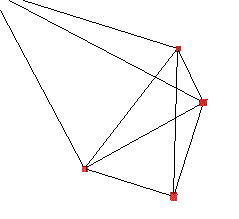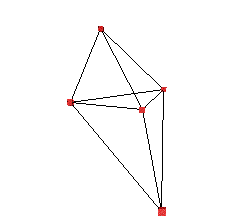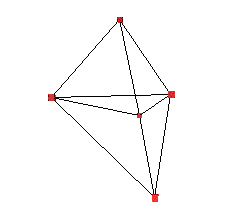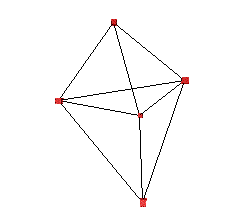
So, my simplified version of a wheel will be four masses connected to an axle, and to each other, by springs. The forces in the springs will effectively represent tensions in the wheel. I'll add a force due to gravity (pointing downwards) and the force on each spring will be represented by Hooke's law. This simplified model already has 24 variables! Three position and three velocities (in 3-d) for each mass.

You can derive the equations of motion either using standard Newtonian forces, or a little more neatly using a Lagrangian approach, but I won't write the equations here, but will save them for another post.

So here's my basic wheel. All I've done here is stretch the springs and let the thing oscillate a little Don't forget that gravity is acting downwards, which is why it is asymmetric.

OK, we can remove the stretch. But how is this a wheel. Well, let's give one of the masses a tangential push. Let's take the black mass and push it upwards.

The net effect is that the entire distribution of masses starts to move, and the wheel is rotating. Of course, it looks a little springy and bouncy, but it's how a real wheel works; all the internal masses of the wheel are talking to one another through internal forces. If we tighten up the springs a little, we can get it to be less bouncy.

Excellent. Well, at the start! But then things go pear-shaped! What's happening? Integration errors, that's what! Basically, I am using a Michael-Mouse integration scheme for these initial tests (and Euler scheme for those in the know) and small errors build up rapidly. What we end up with is energy not being conserved and madness ensuing.

But we can fix this up with a better integration scheme. I'm going to leave that to next time :)