Shooting relativistic fish in a rational barrel
I need to take a breather from grant writing, which is consuming almost every waking hour in between all of the other things that I still need to do. So see this post as a cathartic exercise.
What makes a scientist? Is it the qualification? What you do day-to-day? The association and societies to which you belong? I think a unique definition may be impossible as there is a continuum of properties of scientists. This makes it a little tricky for the lay-person to identify "real science" from "fringe science" (but, in all honesty, the distinction between these two is often not particularly clear cut).
One thing that science (and many other fields) do is have meetings, conferences and workshops to discuss their latest results. Some people seem to spend their lives flitting between exotic locations essentially presenting the same talk to almost the same audience, but all scientists probably attend a conference or two per year.
In one of my own fields, namely cosmology, there are lots of conferences per year. But accompanying these there are another set of conferences going on, also on cosmology and often including discussions of gravity, particle physics, and the power of electricity in the Universe. At these meetings, the words "rational" and "logical" are bandied about, and it is clear that the people attending think that the great mass of astronomer and physicists have gotten it all wrong, are deluded, are colluding to keep the truth from the public for some bizarre agenda - some sort of worship of Einstein and "mathemagics" (I snorted with laughter when I heard this).
If I am being paid to lie to the public, I would like to point out that my cheque has not arrived and unless it does shortly I will go to the papers with a "tell all"!!
These are not a new phenomenon, but were often in shadows. But now, of course, with the internet, any one can see these conference in action with lots of youtube clips and lectures.
Is there any use for such videos? I think so, as, for the student of physics, they present an excellent place to tests one knowledge by identifying just where the presenters are straying off the path.
A brief search of youtube will turn up talks that point out that black holes cannot exist because
is the starting point for the derivation of the Schwarzschild solution.
Now, if you are not really familiar with the mathematics of relativity, this might look quite convincing. The key point is this equation
Roughly speaking, this says that space-time geometry (left-hand side) is related to the matter and energy density (right-hand side, and you calculate the Schwarzschild geometry for a black hole by setting the right-hand side equal to zero.
Now, with the right-hand side equal to zero that means there is no energy and mass, and the conclusion in the video says that there is no source, no thing to produce the bending of space-time and hence the effects of gravity. So, have the physicists been pulling the wool over everyones eyes for almost 100 years?
Now, a university level student may not have done relativity yet, but it should be simple to see the flaw in this argument. And, to do this, we can use the wonderful world of classical mechanics.
In classical physics, where gravity is a force and we deal with potentials, we have a similar equation to the relativistic equation above. It's known as Poisson's equation
The left-hand side is related to derivatives of the gravitational potential, whereas the right-hand side is some constants (including Newton's gravitational constant (G)) and the density given by the rho.
I think everyone is happy with this equation. Now, one thing you calculate early on in gravitational physics is that the gravitational potential outside of a massive spherical object is given by
Note that we are talking about the potential is outside of the spherical body (the simple V and Phi are meant to be the same thing). So, if we plug this potential into Poisson's equation, does it give us a mass distribution which is spherical?
Now, Poisson's equation can look a little intimidating, but let's recast the potential in Cartesian coordinates. Then it looks like this
Ugh! Does that make it any easier? Yes, let's just simply plug it into Wolfram Alpha to do the hard work. So, the derivatives have an x-part, y-part and z-part - here's the x-part.
What makes a scientist? Is it the qualification? What you do day-to-day? The association and societies to which you belong? I think a unique definition may be impossible as there is a continuum of properties of scientists. This makes it a little tricky for the lay-person to identify "real science" from "fringe science" (but, in all honesty, the distinction between these two is often not particularly clear cut).
One thing that science (and many other fields) do is have meetings, conferences and workshops to discuss their latest results. Some people seem to spend their lives flitting between exotic locations essentially presenting the same talk to almost the same audience, but all scientists probably attend a conference or two per year.
In one of my own fields, namely cosmology, there are lots of conferences per year. But accompanying these there are another set of conferences going on, also on cosmology and often including discussions of gravity, particle physics, and the power of electricity in the Universe. At these meetings, the words "rational" and "logical" are bandied about, and it is clear that the people attending think that the great mass of astronomer and physicists have gotten it all wrong, are deluded, are colluding to keep the truth from the public for some bizarre agenda - some sort of worship of Einstein and "mathemagics" (I snorted with laughter when I heard this).
If I am being paid to lie to the public, I would like to point out that my cheque has not arrived and unless it does shortly I will go to the papers with a "tell all"!!
These are not a new phenomenon, but were often in shadows. But now, of course, with the internet, any one can see these conference in action with lots of youtube clips and lectures.
Is there any use for such videos? I think so, as, for the student of physics, they present an excellent place to tests one knowledge by identifying just where the presenters are straying off the path.
A brief search of youtube will turn up talks that point out that black holes cannot exist because
is the starting point for the derivation of the Schwarzschild solution.
Roughly speaking, this says that space-time geometry (left-hand side) is related to the matter and energy density (right-hand side, and you calculate the Schwarzschild geometry for a black hole by setting the right-hand side equal to zero.
Now, with the right-hand side equal to zero that means there is no energy and mass, and the conclusion in the video says that there is no source, no thing to produce the bending of space-time and hence the effects of gravity. So, have the physicists been pulling the wool over everyones eyes for almost 100 years?
Now, a university level student may not have done relativity yet, but it should be simple to see the flaw in this argument. And, to do this, we can use the wonderful world of classical mechanics.
In classical physics, where gravity is a force and we deal with potentials, we have a similar equation to the relativistic equation above. It's known as Poisson's equation
The left-hand side is related to derivatives of the gravitational potential, whereas the right-hand side is some constants (including Newton's gravitational constant (G)) and the density given by the rho.
I think everyone is happy with this equation. Now, one thing you calculate early on in gravitational physics is that the gravitational potential outside of a massive spherical object is given by
Note that we are talking about the potential is outside of the spherical body (the simple V and Phi are meant to be the same thing). So, if we plug this potential into Poisson's equation, does it give us a mass distribution which is spherical?
Now, Poisson's equation can look a little intimidating, but let's recast the potential in Cartesian coordinates. Then it looks like this
Ugh! Does that make it any easier? Yes, let's just simply plug it into Wolfram Alpha to do the hard work. So, the derivatives have an x-part, y-part and z-part - here's the x-part.
Again, is you are a mathphobe, this is not much better, but let's add the y- and z-parts.
After all that, the result is zero! Zilch! Nothing! This must mean that Poisson's equation for this potential is
So, the density is equal to zero. Where's the mass that produces the gravitational field? This is the same as the apparent problem with relativity. What Poisson's equation tells us that the derivatives o the potential AT A POINT is related to the density AT THAT POINT!
Now, remember these are derivatives, and so the potential can have a whole bunch of shapes at that point, as long as the derivatives still hold. One of these, of course, is there being no mass there and so no gravitational potential at all, but any vacuum, with no mass, will above Poisson = 0 equation, including the potential outside of any body (the one used in this example relied on a spherical source).
So, the relativistic version is that the properties of the space-time curvature AT A POINT is related to the mass and energy AT A POINT. A flat space-time is produced when there is no mass and energy, and so has G=0, but so does any point in a vacuum, but that does not mean that the space-time at that point is not curved (and so no gravity).
Anyway, I got that off my chest, and my Discovery Project submitted, but now it's time to get on with a LIEF application!

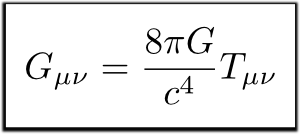







In the classical case the Laplacian of the potential isn't zero everywhere, in the limit of a point mass it diverges at the location of the mass. Is something similar true in GR?
ReplyDeleteYes! The singularity in GR is similar to the singularity in classical physics and Poisson's equation.
ReplyDeleteI'd like to congratulate Cusp on this post, this is exceptionally well explained. I'd just like to add one point on the analogies between classical and relativistic gravity. Of course the second derivatives d_i d_j Phi of the gravitational potential Phi are linked to the source rho and the only way to do this which is invariant under rotations is to take the trace d_i d_i Phi, which just gives the Poisson equation. But as pointed out, d_i d_i Phi = 0 would not imply a constant potential, it only means that there's no mass at that particular point, which emphasises the local relationship between field and source. One could construct a second invariant d_i d_j Phi d_j d_i Phi, which is scalar and which is computed from all tidal shear components: this would measure the variation of the potential and would be nonzero away from field generating masses. In relativity, I think that these two invariants would correspond to the Ricci-scalar (the first) and the invariant curvature (the second).
ReplyDeletehappy kiss day quotes for wife
ReplyDeletekiss day wallpaper with quotes
hug day images and messages
happy hug day funny images